Analysis of Recursion
Let’s go through some examples to get a hang of how to derive time taken for recursive functions.
Python
def fun(n):
if n <= 1:
return
for i in range(n): # 𝛳(n)
print("something")
fun(n//2) # T(n/2)
fun(n//2) # T(n/2)
JavaScript
function fun(n) {
if(n <= 1) {
return;
}
for(let i = 0; i < n; i++) {
console.log('something');
}
fun(Math.floor(n/2));
fun(Math.floor(n/2));
}
Time taken:
Base case:
Python
def fun(n):
if n <= 1:
return
print("something") # 𝛳(1)
fun(n//2) # T(n/2)
fun(n//2) # T(n/2)
JavaScript
function fun(n) {
if(n <= 1) {
return;
}
console.log('something');
fun(Math.floor(n/2));
fun(Math.floor(n/2));
}
Time taken:
Base case:
Python
def fun(n):
if n <= 0:
return
print(n) # 𝛳(1)
fun(n - 1) # T(n - 1)
JavaScript
function fun(n) {
if(n <= 0) {
return;
}
console.log(n);
fun(n - 1);
}
Time taken:
Base case:
Once the value of is written recursively, we can use Recursion Tree Method to find the actual value of . Here are the steps for it:
- Write non-recursive part as root of tree and recursive parts as children.
- Keep expanding children until a pattern emerges.
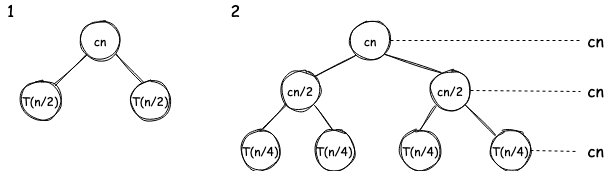
work is being done at every level.
The work is getting reduced by half in each recursion. Therefore the height of tree is
.
Total work done:
.
Therefore, the time complexity is
.
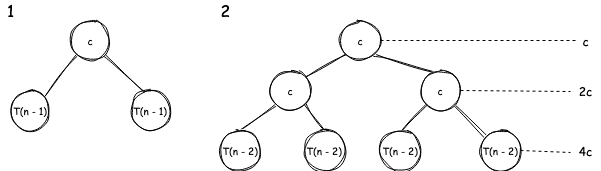
We are reducing by 1 in each recursion, therefore the height of tree will be
.
Total work done:
times.
It’s a geometric progression:
.
Therefore, the time complexity is
.
Formula for geometric progression:
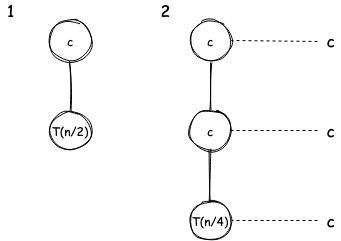
Total work done:
times.
Therefore, the time complexity is
.
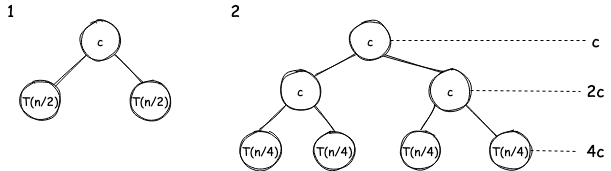
Total work done:
times.
Therefore, the time complexity is .
We can still use Recursion Tree method for incomplete trees, but instead of exact bound we’ll get upper bound.
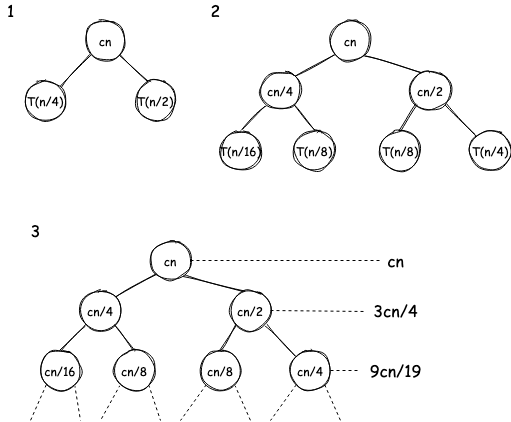
In this example, the left subtree will reduce faster than the right one.
We’ll assume this is a full tree and therefore will get upper bound
instead of the exact bound
.
Total work done: and height of tree is .
It’s a geometric progression with ratio less than 1.
Formula for geometric progression with ratio < 1:
applying geometric progression formula
ignoring constants, the complexity is
The time complexity is .
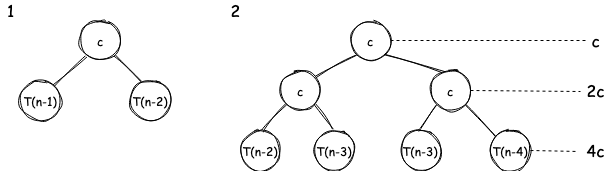
It’s not a full tree with height
.
Total work done:
.
It’s a geometric progression:
.
Therefore, the time complexity is
.